Continued fraction
In mathematics, a finite continued fraction is an expression such as
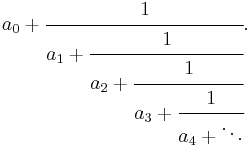
or any analogously defined longer expression, where a0 is an integer and all the other numbers ai are positive integers. If an infinite sequence (a0, a1, a2,...) of such integers is given, the sequence of these expressions defines an infinite continued fraction, which is often written as
Continued fractions, finite and infinite, have a number of remarkable properties related to the Euclidean algorithm for integers or real numbers. Every rational number p/q has two closely related expressions as a finite continued fraction, whose coefficients ai can be determined by applying the Euclidean algorithm to (p,q). The sequence of rational numbers given by any infinite continued fraction converges to an irrational number, which limit is taken to be the value of the continued fraction. Moreover, every irrational number α is the value of a unique infinite continued fraction, whose coefficients can be found using the non-terminating version of the Euclidean algorithm applied to the incommensurable values α and 1. This way of expressing (rational and irrational) real numbers is called their continued fraction representation.
If the partial numerators and partial denominators are allowed to assume arbitrary values, which may in some contexts include functions, the resulting expression is a generalized continued fraction. When it is necessary to distinguish the standard form above from generalized continued fractions, it may be called a simple or regular continued fraction, or is said to be in canonical form.
The term "continued fraction" may also refer to representations of rational functions, arising in their analytic theory. For this use of the term see Padé approximation and Chebyshev rational functions.
Motivation
The study of continued fractions is motivated by a desire to have a "mathematically pure" representation for the real numbers.
Most people are familiar with the decimal representation of real numbers, which may be defined by
where a0 may be any integer, and every other ai is an element of {0, 1, 2, ..., 9}. In this representation, the number π, for example, is represented by the sequence of integers (ai) = (3, 1, 4, 1, 5, 9, 2, ...).
This decimal representation has some problems. One problem is that many rational numbers lack finite representations in this system. For example, the number 1/3 is represented by the infinite sequence (0, 3, 3, 3, 3, ....). Another problem is that the constant 10 is an essentially arbitrary choice, and one which biases the resulting representation toward numbers that have some relation to the integer 10. For example, 137/1600 has a finite decimal representation, while 1/3 does not, not because 137/1600 is simpler than 1/3, but because 1600 happens to divide a power of 10 (106 = 1600 × 625). Continued fraction notation is a representation of the real numbers that avoids both these problems.
Let us consider how we might describe a number like 415/93, which is around 4.4624. This is approximately 4. Actually it is a little bit more than 4, about 4 + 1/2. But the 2 in the denominator is not correct; the correct denominator is a little bit more than 2, about 2 + 1/6, so 415/93 is approximately 4 + 1/(2 + 1/6). But the 6 in the denominator is not correct; the correct denominator is a little bit more than 6, actually 6+1/7. So 415/93 is actually 4+1/(2+1/(6+1/7)). This is exact.
Dropping the redundant parts of the expression 4 + 1/(2 + 1/(6 + 1/7)) gives the abbreviated notation [4; 2, 6, 7]. (Note that it is customary to replace only the first comma by a semicolon.)
The continued fraction representation of real numbers can be defined in this way. It has several desirable properties:
- The continued fraction representation for a number is finite if and only if the number is rational.
- Continued fraction representations for "simple" rational numbers are usually short.
- Every rational number has an essentially unique continued fraction representation. Each rational can be represented in exactly two ways, since [a0; a1, ... an - 1, an] = [a0; a1, ... an - 1, an - 1, 1]. Mathematicians prefer to have a one to one correspondence between rational numbers and continued fractions; the first, shorter one is then chosen as the canonical representation.
- The continued fraction representation of an irrational number is unique.
- The terms of a continued fraction will repeat if and only if it is the continued fraction representation of a quadratic irrational, that is, a real solution to a quadratic equation with integer coefficients.[1] For example, the repeating continued fraction [1; 1, 1, 1, ...] is the golden ratio, and the repeating continued fraction [1; 2, 2, 2, ...] is the square root of 2.
- Truncating the continued fraction representation of a number x early yields a rational approximation for x which is in a certain sense the "best possible" rational approximation (see theorem 5, corollary 1 below for a formal statement).
This last property is extremely important, and is not true of the conventional decimal representation. Truncating the decimal representation of a number yields a rational approximation of that number, but not usually a very good approximation. For example, truncating 1/7 = 0.142857... at various places yields approximations such as 142/1000, 14/100, and 1/10. But clearly the best rational approximation is "1/7" itself. Truncating the decimal representation of π yields approximations such as 31415/10000 and 314/100. The continued fraction representation of π begins [3; 7, 15, 1, 292, ...]. Truncating this representation yields the excellent rational approximations 3, 22/7, 333/106, 355/113, 103993/33102, ... The denominators of 314/100 and 333/106 are almost the same, but the error in the approximation 314/100 is nineteen times as large as the error in 333/106. As an approximation to π, [3; 7, 15, 1] is more than one hundred times more accurate than 3.1416.
Calculating continued fraction representations
Consider a real number r0. Let a0 be the integer part and f0 the fractional part of r0. Then the continued fraction representation of r0 is [a0; a1, a2,...], where [a1; a2,...] is the continued fraction representation of 1/f0.
To calculate a continued fraction representation of a number r0, write down the integer part (technically the floor) of r0. Subtract this integer part from r0. If the difference is 0, stop; otherwise find the reciprocal of the difference and repeat. The procedure will halt if and only if r0 is rational.
-
Find the canonical continued fractions for 3.645 (= 3645/1000), −3.645 (= −3645/1000), and 0 Real number Integer part (floor) Fractional part Reciprocal Canonical continued fraction form r0 = 3645/1000 a0 = 3 f0 = 645/1000 1/f0 = 1000/645 ![\begin{matrix}
3.645 & = & 3 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{4 + \cfrac{1}{2 + \cfrac{1}{6}}}}}} \\
& = & [3; 1, 1, 1, 4, 2, 6]
\end{matrix}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/02874568a184d7e0e7b0646ebea26ff6.png)
r1 = 1000/645 a1 = 1 f1 = 355/645 1/f1 = 645/355 r2 = 645/355 a2 = 1 f2 = 290/355 1/f2 = 355/290 r3 = 355/290 a3 = 1 f3 = 65/290 1/f3 = 290/65 r4 = 290/65 a4 = 4 f4 = 30/65 1/f4 = 65/30 r5 = 65/30 a5 = 2 f5 = 5/30 1/f5 = 30/5 r6 = 30/5 a6 = 6 f6 = 0/5 stop r0 = −3645/1000 a0 = −4 f0 = 355/1000 1/f0 = 1000/355 ![\begin{matrix}
-3.645 & = & -4 + \cfrac{1}{2 + \cfrac{1}{1 + \cfrac{1}{4 + \cfrac{1}{2 + \cfrac{1}{6}}}}} \\
& = & [-4; 2, 1, 4, 2, 6]
\end{matrix}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/5c24cd58f6062250355085682b0afa81.png)
r1 = 1000/355 a1 = 2 f1 = 290/355 1/f1 = 355/290 r2 = 355/290 a2 = 1 f2 = 65/290 1/f2 = 290/65 r3 = 290/65 a3 = 4 f3 = 30/65 1/f3 = 65/30 r4 = 65/30 a4 = 2 f4 = 5/30 1/f4 = 30/5 r3 = 30/5 a3 = 6 f3 = 0/5 stop r0 = 0 a0 = 0 f0 = 0 stop ![0 = [0]\,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/c0710e6cde03581bbc6f08a870d30f01.png)
The number 3.645 can also be represented by the continued fraction expansion [3; 1, 1, 4, 2, 5, 1]; refer to Finite continued fractions below.
This algorithm is suitable for all real numbers, but the limited precision of floating point numbers will often lead to small errors, skewing the final result. Instead, floating point numbers should be converted to rational numbers before processing. The denominator is usually a power of two on modern computers, and a power of ten on electronic calculators, so basic Euclidian divisions can be used directly (the Euclid GCD algorithm may be optionally be used to simplify the intermediate fractions, but this is not needed to compute all the terms of the continued fraction).
This algorithm works as well for negative numbers, but the beginning terms in of the continued fraction expansion are different.
Modified algorithm for shorter expansions
If the integer part function is chosen so that that it selects the integer quotient an that best approximates the real number rn at each step (instead of choosing the floor function in the canonical algorithm above), so that the remainder fractional term fn will be at most half of unity in absolute value, i.e.
it will generate shorter expansions that may converge faster (with less terms). However, the fractional terms may become positive or negative, and then this will also apply to the next terms an of the expansion. This algorithm works as well with any negative real numbers.
With such modification of the algorithm, we get :
-
Find the shortest continued fractions for 3.645 (= 3645/1000), −3.645 (= −3645/1000), and 0 Real number Integer part (nearest) Fractional part Reciprocal Shortest continued fraction form r0 = 3645/1000 a0 = 4 f0 = −355/1000 1/f0 = −1000/355 ![\begin{matrix}
3.645 & = & 4 + \cfrac{1}{-3 + \cfrac{1}{5 + \cfrac{1}{2 + \cfrac{1}{6}}}} \\
& = & [4; -3, 5, 2, 6]
\end{matrix}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/17545fdc4dd6c02756a34fd4e4fc0cc8.png)
r1 = −1000/355 a1 = −3 f1 = 65/355 1/f1 = 355/65 r2 = 355/65 a2 = 5 f2 = 30/65 1/f2 = 65/30 r3 = 65/30 a3 = 2 f3 = 5/30 1/f3 = 30/5 r4 = 30/5 a4 = 6 f4 = 0/5 stop r0 = −3645/1000 a0 = −4 f0 = 355/1000 1/f0 = 1000/355 ![\begin{matrix}
-3.645 & = & -4 + \cfrac{1}{3 + \cfrac{1}{-5 + \cfrac{1}{-2 + \cfrac{1}{-6}}}} \\
& = & [-4; 3, -5, -2, -6]
\end{matrix}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/c0fcf55a700dc311f8cc70cd918ca48a.png)
r1 = 1000/355 a1 = 3 f1 = −65/355 1/f1 = −355/65 r2 = −355/65 a2 = −5 f2 = −30/65 1/f2 = −65/30 r3 = −65/30 a3 = −2 f3 = −5/30 1/f3 = −30/5 r4 = −30/5 a4 = −6 f4 = 0/5 stop r0 = 0 a0 = 0 f0 = 0 stop ![0 = [0]\,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/c0710e6cde03581bbc6f08a870d30f01.png)
This algorithm produces the shortest continued fraction expansion for negative numbers, where all its terms are the negation of the terms in the shortest continued fraction expansion of the opposite positive numbers, with also exactly the same number of terms.
Notations for continued fractions
The integers a0, a1, etc., are called the quotients of the continued fraction. One can abbreviate a continued fraction as
or, in the notation of Pringsheim, as
Note that in the canonical continued fraction form, only the first integer term may be negative or null, and all the remaining terms are strictly positive integers, the last one being always greater than one.
Here is another related notation:
Sometimes angle brackets are used, like this:
The semicolon in the square and angle bracket notations is sometimes replaced by a comma.
One may also define infinite simple continued fractions as limits:
This limit exists for any choice of positive integers a0, a1, ... .
Finite continued fractions
Every finite continued fraction represents a rational number, and every rational number can be represented in precisely two different ways as a finite continued fraction. These two representations agree except in their final terms. In the longer representation the final term in the continued fraction is 1; the shorter representation drops the final 1, but increases the new final term by 1. The final element in the short representation is therefore always greater than 1, if present. In symbols:
For example,
Note that in the canonical finite continued fraction form, only the first integer term may be negative or null, and all the remaining terms are strictly positive integers.
Continued fractions of reciprocals
The continued fraction representations of a positive rational number and its reciprocal are identical except for a shift one place left or right depending on whether the number is less than or greater than one respectively. In other words, the numbers represented by ![[a_0;a_1,a_2,a_3,\ldots,a_n]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/371951e599137b2a4dc77b15f08da9f7.png) and
and ![[0;a_0,a_1,a_2,\ldots,a_n]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/ec441968137bb5480ee35884c3ceea36.png) are reciprocals. This is because if
are reciprocals. This is because if  is an integer then if
is an integer then if 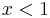 then
then 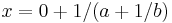 and
and 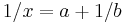 and if
and if 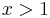 then
then 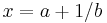 and
and 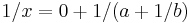 with the last number that generates the remainder of the continued fraction being the same for both
with the last number that generates the remainder of the continued fraction being the same for both 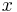 and its reciprocal.
and its reciprocal.
For example,
Infinite continued fractions
Every infinite continued fraction is irrational, and every irrational number can be represented in precisely one way as an infinite continued fraction.
An infinite continued fraction representation for an irrational number is mainly useful because its initial segments provide excellent rational approximations to the number. These rational numbers are called the convergents of the continued fraction. Even-numbered convergents are smaller than the original number, while odd-numbered ones are bigger.
For a continued fraction [a0; a1, a2, ...], the first four convergents (numbered 0 through 3) are
In words, the numerator of the third convergent is formed by multiplying the numerator of the second convergent by the third quotient, and adding the numerator of the first convergent. The denominators are formed similarly. Therefore, each convergent can be expressed explicitly in terms of the continued fraction as the ratio of certain multivariate polynomials called continuants.
If successive convergents are found, with numerators h1, h2, ... and denominators k1, k2, ... then the relevant recursive relation is:

The successive convergents are given by the formula
Thus to incorporate a new term into a rational approximation, only the two previous convergents are necessary. The initial "convergents" (required for the first two terms) are 0⁄1 and 1⁄0. For example, here are the convergents for [0;1,5,2,2].
-
n −2 −1 0 1 2 3 4 an 0 1 5 2 2 hn 0 1 0 1 5 11 27 kn 1 0 1 1 6 13 32
Some useful theorems
If a0, a1, a2, ... is an infinite sequence of positive integers, define the sequences 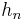 and
and 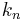 recursively:
recursively:
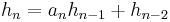 |
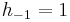 |
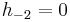 |
|||
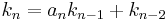 |
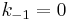 |
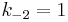 |
Theorem 1
For any positive 
Theorem 2
The convergents of [a0; a1, a2, ...] are given by
Theorem 3
If the nth convergent to a continued fraction is 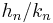 , then
, then
Corollary 1: Each convergent is in its lowest terms (for if 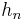 and
and 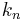 had a nontrivial common divisor it would divide
had a nontrivial common divisor it would divide 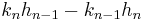 , which is impossible).
, which is impossible).
Corollary 2: The difference between successive convergents is a fraction whose numerator is unity:
Corollary 3: The continued fraction is equivalent to a series of alternating terms:
Corollary 4: The matrix
has determinant plus or minus one, and thus belongs to the group of 2x2 unimodular matrices 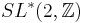 .
.
Theorem 4
Each (sth) convergent is nearer to a subsequent (nth) convergent than any preceding (rth) convergent is. In symbols, if the nth convergent is taken to be ![[a_0;a_1,a_2,\ldots a_n]=x_n](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/ae1e4ae3bd78e70fbdfdcd86423f72d8.png) , then
, then
for all r < s < n.
Corollary 1: the even convergents (before the nth) continually increase, but are always less than xn.
Corollary 2: the odd convergents (before the nth) continually decrease, but are always greater than xn.
Theorem 5
Corollary 1: any convergent is nearer to the continued fraction than any other fraction whose denominator is less than that of the convergent
Corollary 2: any convergent which immediately precedes a large quotient is a near approximation to the continued fraction.
Semiconvergents
If
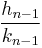 and
and 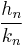
are successive convergents, then any fraction of the form
where a is a nonnegative integer and the numerators and denominators are between the n and n + 1 terms inclusive are called semiconvergents, secondary convergents, or intermediate fractions. Often the term is taken to mean that being a semiconvergent excludes the possibility of being a convergent, rather than that a convergent is a kind of semiconvergent.
The semiconvergents to the continued fraction expansion of a real number x include all the rational approximations which are better than any approximation with a smaller denominator. Another useful property is that consecutive semiconvergents a/b and c/d are such that ad − bc = ±1.
Best rational approximations
A best rational approximation to a real number x is a rational number n/d, d > 0, that is closer to x than any approximation with a smaller denominator. The simple continued fraction for x generates all of the best rational approximations for x according to three rules:
- Truncate the continued fraction, and possibly decrement its last term.
- The decremented term cannot have less than half its original value.
- If the final term is even, a special rule decides if half its value is admissible. (See below.)
For example, 0.84375 has continued fraction [0;1,5,2,2]. Here are all of its best rational approximations.
-
[0;1] [0;1,3] [0;1,4] [0;1,5] [0;1,5,2] [0;1,5,2,1] [0;1,5,2,2] 1 
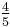
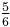
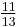
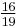
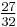
The strictly monotonic increase in the denominators as additional terms are included permits an algorithm to impose a limit, either on size of denominator or closeness of approximation.
One formal description of the half rule is that the halved term, ak/2, is admissible if and only if
The convergents to x are best approximations in an even stronger sense: n/d is a convergent for x if and only if |dx − n| is the least relative error among all approximations m/c with c ≤ d; that is, we have |dx − n| < |cx − m| so long as c < d. (Note also that |dkx − nk| → 0 as k → ∞.)
Comparison of continued fractions
Consider x = [a0; a1, ...] and y = [b0; b1, ...]. If k is the smallest index for which ak is unequal to bk then x < y if (−1)k(ak − bk) < 0 and y < x otherwise.
If there is no such k, but one expansion is shorter than the other, say x = [a0; a1, ..., an] and y = [b0; b1, ..., bn, bn+1, ...] with ai = bi for 0 ≤ i ≤ n, then x < y if n is even and y < x if n is odd.
Continued fraction expansions of π
To calculate the convergents of pi we may set 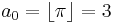 , define
, define 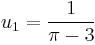
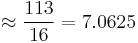 and
and 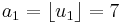 ,
, 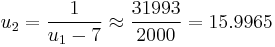 and
and 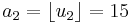 ,
, 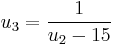
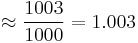 . Continuing like this, one can determine the infinite continued fraction of π as [3; 7, 15, 1, 292, 1, 1, ...]. The third convergent of π is [3; 7, 15, 1] = 355/113 = 3.14159292035..., which is fairly close to the true value of π.
. Continuing like this, one can determine the infinite continued fraction of π as [3; 7, 15, 1, 292, 1, 1, ...]. The third convergent of π is [3; 7, 15, 1] = 355/113 = 3.14159292035..., which is fairly close to the true value of π.
Let us suppose that the quotients found are, as above, [3; 7, 15, 1]. The following is a rule by which we can write down at once the convergent fractions which result from these quotients without developing the continued fraction.
The first quotient, supposed divided by unity, will give the first fraction, which will be too small, namely, 3/1. Then, multiplying the numerator and denominator of this fraction by the second quotient and adding unity to the numerator, we shall have the second fraction, 22/7, which will be too large. Multiplying in like manner the numerator and denominator of this fraction by the third quotient, and adding to the numerator the numerator of the preceding fraction, and to the denominator the denominator of the preceding fraction, we shall have the third fraction, which will be too small. Thus, the third quotient being 15, we have for our numerator (22 × 15 = 330) + 3 = 333, and for our denominator, (7 × 15 = 105) + 1 = 106. The third convergent, therefore, is 333/106. We proceed in the same manner for the fourth convergent. The fourth quotient being 1, we say 333 times 1 is 333, and this plus 22, the numerator of the fraction preceding, is 355; similarly, 106 times 1 is 106, and this plus 7 is 113.
In this manner, by employing the four quotients [3; 7, 15, 1], we obtain the four fractions:
These convergents are alternately smaller and larger than the true value of π, and approach nearer and nearer to π. The difference between a given convergent and π is less than the reciprocal of the product of the denominators of that convergent and the next convergent. For example, the fraction 22/7 is greater than π, but 22/7 − π is less than 1/(7×106), that is 1/742 (in fact, 22/7 − π is just less than 1/790).
The demonstration of the foregoing properties is deduced from the fact that if we seek the difference between one of the convergent fractions and the next adjacent to it we shall obtain a fraction of which the numerator is always unity and the denominator the product of the two denominators. Thus the difference between 22/7 and 3/1 is 1/7, in excess; between 333/106 and 22/7, 1/742, in deficit; between 355/113 and 333/106, 1/11978, in excess; and so on. The result being, that by employing this series of differences we can express in another and very simple manner the fractions with which we are here concerned, by means of a second series of fractions of which the numerators are all unity and the denominators successively be the product of every two adjacent denominators. Instead of the fractions written above, we have thus the series:
The first term, as we see, is the first fraction; the first and second together give the second fraction, 22/7; the first, the second and the third give the third fraction 333/106, and so on with the rest; the result being that the series entire is equivalent to the original value.
The sequence of partial denominators of the simple continued fraction of π does not show any obvious pattern:[3]
![\pi=[3;7,15,1,292,1,1,1,2,1,3,1,14,2,1,1,2,2,2,2,1,84,\cdots]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/108f4286d5ad19cd2d6aa6910dbe7431.png)
- or

However, there are generalized continued fractions for π with a perfectly regular structure, such as:
Other continued fraction expansions
Periodic continued fractions
The numbers with periodic continued fraction expansion are precisely the irrational solutions of quadratic equations with rational coefficients (rational solutions have finite continued fraction expansions as previously stated). The simplest examples are the golden ratio φ = [1; 1, 1, 1, 1, 1, ...] and √ 2 = [1; 2, 2, 2, 2, ...]; while √14 = [3;1,2,1,6,1,2,1,6...] and √42 = [6;2,12,2,12,2,12...]. All irrational square roots of integers have a special form for the period; a symmetrical string, like the empty string (for √ 2) or 1,2,1 (for √14), followed by the double of the leading integer.
A property of the golden ratio φ
An interesting result, stemming from the fact that the continued fraction expansion for φ doesn't use any integers greater than 1, is that φ is one of the most "difficult" real numbers to approximate with rational numbers. One theorem[4] states that any real number k can be approximated by rational m/n with
While virtually all real numbers k will eventually have infinitely many convergents m/n whose distance from k is significantly smaller than this limit, the convergents for φ (i.e., the numbers 5/3, 8/5, 13/8, 21/13, etc.) consistently "toe the boundary", keeping a distance of almost exactly 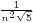 away from φ, thus never producing an approximation nearly as impressive as, for example, 355/113 for π. It can also be shown that every real number of the form (a + bφ)/(c + dφ) – where a, b, c, and d are integers such that ad − bc = ±1 – shares this property with the golden ratio φ.
away from φ, thus never producing an approximation nearly as impressive as, for example, 355/113 for π. It can also be shown that every real number of the form (a + bφ)/(c + dφ) – where a, b, c, and d are integers such that ad − bc = ±1 – shares this property with the golden ratio φ.
Regular patterns in continued fractions
While one cannot discern any pattern in the simple continued fraction expansion of π, this is not true for e, the base of the natural logarithm:
which is a special case of this general expression for positive integer n:
Another, more complex pattern appears in this continued fraction expansion for positive odd n:
with a special case for n = 1:
Other continued fractions of this sort are
where n is a positive integer; also, for integral n:
with a special case for n = 1:
If In(x) is the modified, or hyperbolic, Bessel function of the first kind, we may define a function on the rationals p/q by
which is defined for all rational numbers, with p and q in lowest terms. Then for all nonnegative rationals, we have
with similar formulas for negative rationals; in particular we have
Many of the formulas can be proved using Gauss's continued fraction.
Typical continued fractions
Most irrational numbers do not have any periodic or regular behavior in their continued fraction expansion. Nevertheless Khinchin proved that for almost all real numbers x, the ai (for i = 1, 2, 3, ...) have an astonishing property: their geometric mean is a constant (known as Khinchin's constant, K ≈ 2.6854520010...) independent of the value of x. Paul Lévy showed that the nth root of the denominator of the nth convergent of the continued fraction expansion of almost all real numbers approaches an asymptotic limit, which is known as Lévy's constant. Lochs' theorem states that nth convergent of the continued fraction expansion of almost all real numbers determines the number to an average accuracy of just over n decimal places.
Pell's equation
Continued fractions play an essential role in the solution of Pell's equation. For example, for positive integers p and q, p2 − 2q2 = ±1 if and only if p/q is a convergent of √2.
Continued fractions and chaos
Continued fractions also play a role in the study of chaos, where they tie together the Farey fractions which are seen in the Mandelbrot set with Minkowski's question mark function and the modular group Gamma.
The backwards shift operator for continued fractions is the map 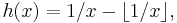 called the Gauss map, which lops off digits of a continued fraction expansion:
called the Gauss map, which lops off digits of a continued fraction expansion: ![h([0;a_1,a_2,a_3,\dots]) = [0;a_2,a_3,\dots]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/89681ecc87ecc413155afda307335c77.png) . The transfer operator of this map is called the Gauss-Kuzmin-Wirsing operator. The distribution of the digits in continued fractions is given by the zero'th eigenvector of this operator, and is called the Gauss-Kuzmin distribution.
. The transfer operator of this map is called the Gauss-Kuzmin-Wirsing operator. The distribution of the digits in continued fractions is given by the zero'th eigenvector of this operator, and is called the Gauss-Kuzmin distribution.
Eigenvalues and eigenvectors
The Lanczos algorithm uses a continued fraction expansion to iteratively approximate the eigenvalues and eigenvectors of a large sparse matrix.
History of continued fractions
- 300 BC Euclid's Elements contains an algorithm for the greatest common divisor which generates a continued fraction as a by-product
- 499 The Aryabhatiya contains the solution of indeterminate equations using continued fractions
- 1579 Rafael Bombelli, L'Algebra Opera - method for the extraction of square roots which is related to continued fractions
- 1613 Pietro Cataldi, Trattato del modo brevissimo di trovar la radice quadra delli numeri - first notation for continued fractions
- Cataldi represented a continued fraction as
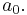 &
&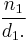 &
&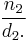 &
&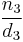 with the dots indicating where the following fractions went.
with the dots indicating where the following fractions went.
- 1695 John Wallis, Opera Mathematica - introduction of the term "continued fraction"
- 1737 Leonhard Euler, De fractionibus continuis dissertatio - Provided the first then-comprehensive account of the properties of continued fractions, and included the first proof that the number e is irrational.[5]
- 1748 Euler, Introductio in analysin infinitorum. Vol. I, Chapter 18 - proved the equivalence of a certain form of continued fraction and a generalized infinite series, proved that every rational number can be written as a finite continued fraction, and proved that the continued fraction of an irrational number is infinite.[6]
- 1761 Johann Lambert - gave the first proof of the irrationality of π using a continued fraction for tan(x).
- 1768 Joseph Louis Lagrange - provided the general solution to Pell's equation using continued fractions similar to Bombelli's
- 1770 Lagrange - proved that quadratic irrationals have a periodic continued fraction expansion
- 1813 Carl Friedrich Gauss, Werke, Vol. 3, pp. 134–138 - derived a very general complex-valued continued fraction via a clever identity involving the hypergeometric function
- 1892 Henri Padé defined Padé approximant
- 1972 Bill Gosper - First exact algorithms for continued fraction arithmetic.
See also
- Stern–Brocot tree
- Computing continued fractions of square roots
- Complete quotient
- Engel expansion
- Mathematical constants (sorted by continued fraction representation)
- Restricted partial quotients
- Infinite series
- Infinite product
- Iterated binary operation
- Euler's continued fraction formula
Notes
- ↑ Weisstein, Eric W., "Periodic Continued Fraction" from MathWorld.
- ↑ Paeth, Alan W. (1995). Graphic Gems V. Academic Press. ISBN 0-12-543455-3.
- ↑ A001203: Continued fraction for Pi, On-Line Encyclopedia of Integer Sequences
- ↑ Theorem 193: Hardy, G.H.; Wright, E.M. (1979). An Introduction to the Theory of Numbers (Fifth ed.). Oxford.
- ↑ Sandifer, Ed (February 2006). "How Euler Did It: Who proved e is irrational?" (PDF). MAA Online. http://www.maa.org/editorial/euler/How%20Euler%20Did%20It%2028%20e%20is%20irrational.pdf.
- ↑ "E101 -- Introductio in analysin infinitorum, volume 1". http://math.dartmouth.edu/~euler/pages/E101.html. Retrieved 2008-03-16.
References
- Jones, William B.; Thron, W. J. (1980). Continued Fractions: Analytic Theory and Applications. Encyclopedia of Mathematics and its Applications.. 11. Addison-Wesley Publishing Company. ISBN 0-201-13510-8.
- A. Ya. Khinchin, Continued Fractions, 1935, English translation University of Chicago Press, 1961 ISBN 0-486-69630-8
- Oskar Perron, Die Lehre von den Kettenbrüchen, Chelsea Publishing Company, New York, NY 1950.
- Andrew M. Rockett and Peter Szusz, Continued Fractions, World Scientific Press, 1992 ISBN 978-9-81-021052-6
- H. S. Wall, Analytic Theory of Continued Fractions, D. Van Nostrand Company, Inc., 1948 ISBN 0-8284-0207-8
- A. Cuyt, V. Brevik Petersen, B. Verdonk, H. Waadeland, W.B. Jones, Handbook of Continued fractions for Special functions, Springer Verlag, 2008 ISBN 978-1-4020-6948-2
External links
- Linas Vepstas Continued Fractions and Gaps (2004) reviews chaotic structures in continued fractions.
- Continued Fractions on the Stern-Brocot Tree at cut-the-knot
- The Antikythera Mechanism I: Gear ratios and continued fractions
- Continued Fraction Arithmetic Gosper's first continued fractions paper, unpublished. Cached on the Internet Archive's Wayback Machine
- Weisstein, Eric W., "Continued Fraction" from MathWorld.
- Continued Fractions by Stephen Wolfram and Continued Fraction Approximations of the Tangent Function by Michael Trott, Wolfram Demonstrations Project.
- Exact Continued Fraction for Pi
- Continued Fractions and Continuants at sputsoft.com
- a view into "fractional interpolation" of a continued fraction {1;1,1,1,...}
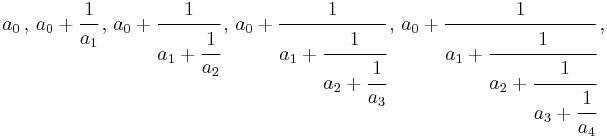
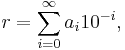
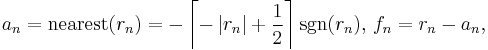
![x = [a_0; a_1, a_2, a_3] \;](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/6382cc2d91f73d44f69895b6d2b3ea06.png)
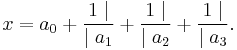
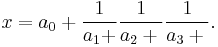
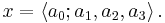
![[a_0; a_1, a_2, a_3, \,\ldots ] = \lim_{n \to \infty} [a_0; a_1, a_2, \,\ldots, a_n].](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/61e8d3912f012f1b1be348b7ffbf1c65.png)
![[a_{0}; a_{1}, a_{2}, \,\ldots, a_{n-1}, a_{n}, 1]=[a_{0}; a_{1}, a_{2}, \,\ldots, a_{n-1}, a_{n} + 1]. \;](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/db718cedfa322845dcaa74020824ec2e.png)
![[a_{0}; 1]=[a_{0} + 1]. \;](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/547cb7aadd150931bed7509ade7a238b.png)
![2.25 = 2 + 1/4 = [2; 4] = [2; 3, 1], \;](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/96ef25cc96b520a542e92960fd1ed677.png)
![-4.2 = -5 + 4/5 = [-5; 1, 4] = [-5; 1, 3, 1]. \;](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/02240fc324c2ac75bef26a841ea48957.png)
![2.25 = \frac{9}{4} = [2; 4], \;](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/3d8f2c12ea520aa1fa2375705fd9e2a6.png)
![\frac{1}{2.25} = \frac{4}{9} = [0; 2, 4]. \;](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/e31b7959b8e322c1758a9830f36656b3.png)
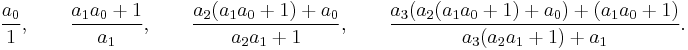
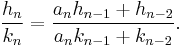
![\left[a_0; a_1, \,\dots, a_{n-1}, x \right]=
\frac{x h_{n-1}+h_{n-2}}
{x k_{n-1}+k_{n-2}}.](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/2121d15f37eb60c326eb9df0b64ff328.png)
![\left[a_0; a_1, \,\dots, a_n\right]=
\frac{h_n}
{k_n}.](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/15b0b6545256be89c8c732a82ea531d7.png)
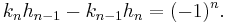
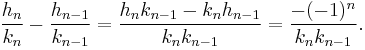
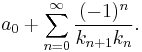
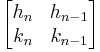
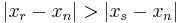
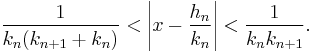
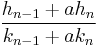
![\left[a_k;a_{k-1},\ldots,a_1\right] > \left[a_k;a_{k+1},\ldots\right].](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/60a0c4401e4ab0fff61df7d03d176968.png)
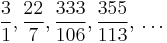
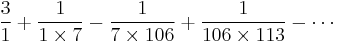
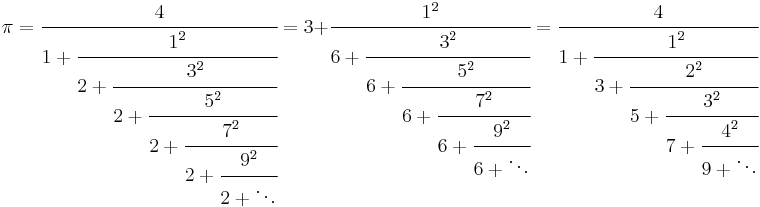
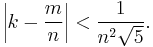
![e = e^1 = [2; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1, 12, 1, 1, \dots] \,\!,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/66ddfce7d2d19f05a2879a850ecd36f4.png)
![e^{1/n} = [1; n-1, 1, 1, 3n-1, 1, 1, 5n-1, 1, 1, 7n-1, 1, 1, \dots] \,\!.](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/5f13d31335a9523858362f121a2f126c.png)
![e^{2/n} = \left[1; \frac{n-1}{2}, 6n, \frac{5n-1}{2}, 1, 1, \frac{7n-1}{2}, 18n, \frac{11n-1}{2}, 1, 1, \frac{13n-1}{2}, 30n, \frac{17n-1}{2}, 1, 1, \dots \right] \,\!,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/0683949bea5673e974674cd4006d503d.png)
![e^2 = [7; 2, 1, 1, 3, 18, 5, 1, 1, 6, 30, 8, 1, 1, 9, 42, 11, 1, 1, 12, 54, 14, 1, 1 \dots, 3k, 12k+6, 3k+2, 1, 1 \dots] \,\!.](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/8edb6388f7ed993f232e03c3e664eee0.png)
![\tanh(1/n) = [0; n, 3n, 5n, 7n, 9n, 11n, 13n, 15n, 17n, 19n, \dots] \,\!](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/34502897a8b91f0f63317e945cd05c4c.png)
![\tan(1/n) = [0; n-1, 1, 3n-2, 1, 5n-2, 1, 7n-2, 1, 9n-2, 1, \dots]\,\!,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/b13814714b1f785a5e14c3b769b23e31.png)
![\tan(1) = [1; 1, 1, 3, 1, 5, 1, 7, 1, 9, 1, 11, 1, 13, 1, 15, 1, 17, 1, 19, 1, \dots]\,\!.](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/0aaa8f9d7d743168e2d967aa05fdce1f.png)
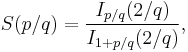
![S(p/q) = [p+q; p+2q, p+3q, p+4q, \dots]\,\!](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/391336ee059ab587dec39619329ba523.png)
![S(0) = S(0/1) = [1; 2, 3, 4, 5, 6, 7, \dots]\,\!.](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/be43953da2efc6e4c733d61faaaac37a.png)